设计师的数学意识
今年 4 月份 Google 和 Adobe 联合发布了思源宋体,继思源黑体之后的又一款开源的泛 CJK 字体,这款高质量的字体对于各行各业的设计师来说无疑是一份馈赠,也是对开源意识的激励。如果初略去审视这款字体,有两个明显的特征,一个是字体的框架结构区别于传统的宋体,更接近黑体,如中宫大、重心低等特征;另一个特征就是字体轮廓的曲线特征,即贝塞尔曲线的绘制结构和策略。思源宋体的轮廓绘制使用了简洁并求效率的方式,除了特殊的笔画,基本采用单条曲线(即头尾两个节点)完成,就像是“丶”,有着较大走势变化的形状,也使用单条曲线绘制完成,这样带来的结果是,过度拉长其中一条曲线的控制点手柄,就像“要”字的长点的尾部,思源宋体就靠单条曲线完成大弧度,选择此种曲线绘制策略应是综合了对效率的考虑,如果只是从形态角度来考虑,这种绘制方式当然不会是最佳的选择。
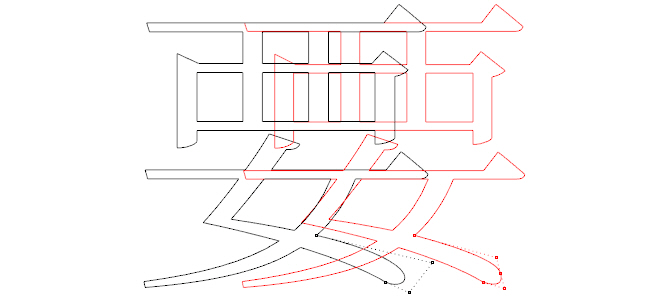
字体在实际场景中的使用,会有不少坑坑洼洼等着设计师去踩。如上图所示的黑红两色的“要”字轮廓,都是使用思源宋体,只不过是在不同设计软件环境中使用,黑色是在 Adobe Illustrator 中使用思源宋体,而红色字是在 Rhino 中使用思源宋体(曲线输入)。黑红两个字,大体上看相差不大,但是如果放大去比较长点的尾部的形态,会发现 Rhino 中的字形明显发生了偏离,如果来对比两者的曲线结构,也能发现两者是不一样的。
如果我们仅停于这,我们就会踩着这些坑坑洼洼跌跌撞撞地往前走。在这些软件中使用字体可以碰到各种问题,这些问题通常不那么明显,就像上图的“要”字,需要放大才能发现一些差别,而且我们可以采用很多补救手段来绕过这些问题,比如重新绘制曲线,碰到产生形变、无法布尔运算等问题,重新绘制一下,或者干脆不在乎这些细微的差别。
上图黑红两个“要”字的形态有偏差,是因为黑字是使用了单条的三次曲线绘制而成,而红字是两段的二次曲线来完成,原因就是 Adobe Illustrator 使用字体的轮廓的类型标准是 PostScript,而 Rhino 等一些三维软件使用的标准是 TrueType,PostScript 的曲线部分使用的是三次贝塞尔曲线,而 TrueType 使用的是二次贝塞尔曲线。当从三次曲线转化到二次曲线时,尽管如上图所示可以用更多的曲线段来组成,但是形态上会有一些损失,而这些损失的大小与原先的三次曲线绘制策略有很大的关系,如同思源宋体的“要”字长点的绘制方式,即过度拉伸曲线的控制点手柄,在曲线阶次从高到底转化过程中就会发生很大的变化,因为软件的算法不会完全倾向与“保持形态不变”而无休止的增加曲线段数。(所以目前如果要在 Rhino 等软件中使用字体轮廓,保守安全的方法就是通过 Illustrator 等软件来作数据导入。)
不只是字体,如果我们日常的工作会使用到一些 CAD 软件来做设计,会碰到很多很多不知道为何发生的问题,这些问题通常可以使用一些迂回的途径来绕过,但如果要想了解一下问题的原由,通常与一些数学概念相关。在实际工作中,我们并不需要去了解这些数学概念的详细情况,但是我们需要去接近,需要具有一些数学的意识。
在使用一个 CAD 软件的过程中,比如说 Rhino,我们去完成一个形态的建模,会使用到各种建线、建面以及很多的编辑工具,工具之多,可以让我们得心应手,达到一个结果可以有很多路径和手段。但是,一旦使用工具越多,那些“不知为何发生”的问题就越多,这些问题让形态总是无法按照自己的想法来,比如形态发生莫名其妙的变化,从实体复制出来的线条无法达到所需要求,布尔运算怎么也实现不了,数据导入导出发生了形态变异……
通常情况,这些问题的最佳解决方法,不是去试一个又一个的可能方案,而是先打开像 Rhino 里的 Details,在 Object Description 中去审查这些形态的属性。
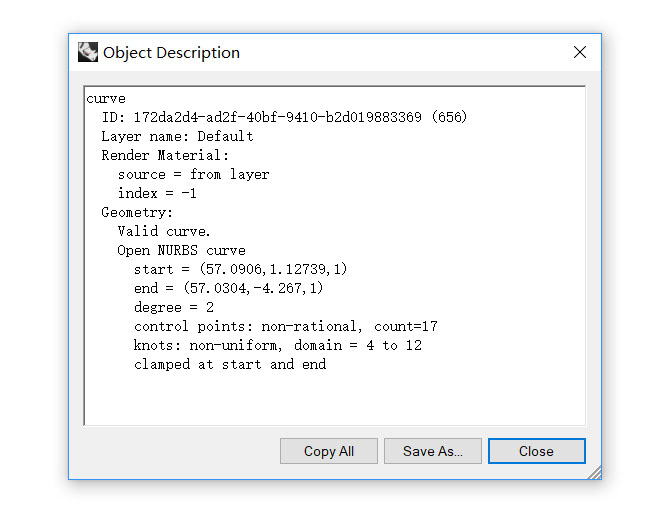
Object Description 窗口中信息并不复杂,比如曲线的属性,最主要就是阶次是多少,控制点是有理还是非有理的,节点是非均匀还是均匀的,其实就是来自于 NURBS 的基本概念,非均匀有理 B 样条,非均匀涵盖了均匀(即均匀是非均匀的一种特殊形态),有理涵盖了非有理(即非有理是有理的一种特殊形态)。而在我们使用多种工具来塑造形态,或者经过导入导出的过程,如果不加注意,曲线或曲面就有可能在阶次、均匀与否和有理与否上发生变化,就给编辑可能带来一些不可描述的问题。比如有理曲线的控制点可以有不同的权重,拉动一个控制点和拉动邻近的控制点对曲线带来的形态变化就不一样,而不像非有理曲线那样每个控制点的权重一样,而控制点怎么去影响曲线就和节点是否均匀有关了,有时碰到曲线变成了非均匀,可能带来编辑结果的不可预知或者复杂性。
但是,对设计师还是专业的建模师,并不需要去了解背后真正的数学内容,需要培养的是理性的意识,尽管这种理性的意识也是来自于经验的积累,但是它必须要触及一些概念,具备“知其所以然”的意识。比如当一条曲线无法完成我们任务时,我们可能会用到“重建曲线”工具,但我们需要知道是去重建什么,而不是试一下看看是否有效果。
像 Alias 在帮助文档中整理了“Alias Golden Rules”(Alias 黄金法则),通过对这些法则的认识和操练,就能培养其理性和数学的意识。
我们可以从一条曲线、一个模型的数学几何结构——诸如控制点的排布——看出设计及其质量,这种结构及其质量也会在最终的产品上表现而出。
:: – ::

传统的样条曲线的绘制以及放样,无论是用于实际尺寸的模板制作,还是缩小的图纸绘制,都是模拟的、类比的、平移式的,一条直线或一条曲线的绘制都是沿着尺子或者木条的边缘画出的,而到了计算机辅助设计的时代,比例不再成为图纸绘制的约束,从小屏幕上的图纸到最终物品的尺寸,从实际物品的尺寸回到小尺寸的图纸,这种放大和缩小接近无损的。
在计算机上,一条直线可以描述成从一个起点指向终点的数学关系,而在现实生活中,这种抽象也在进行之中。对比一下手工业时代对“笔直”的制作,以及现在对“笔直”的生产,当我们将一条直线越做越直,直线度越来越高,精度越来越高,它就愈加抽象化,因为这个直线度已经不足以引起品味了。
我们身边的所有东西的精度都在提高,不只是手边的产品,比如手机,包括更大尺寸的,比如建筑,像 Apple Park 中很多细节就以产品设计的精度来设计和制作(这种追求在传统的视角来看是反建筑学的),这种精度上的发展会一直不停的发展,我们无法预想今后会是怎样。手工艺时代留下饱含温情的触觉,无法平移到现代科技生产的物品之中,现代科技制品有自己的触觉。
而不变的是设计之中的理性,理性的很大一个内容就是数学,Colin Rowe 在《理想别墅的数学》一文开头引用了 Christopher Wren 的话:“美有两种起因:天然性和习惯性。自然美来自构成统一性的几何,即均衡与比例。习惯美来自使用,因为熟悉会使人生发对事物原本没有的爱。后者出错的机会较大。真正的标准应该是自然或几何美。”(城市笔记人的翻译)但是如果去详细地比较,会发现成为规则的理性也都会成为习惯,唯有不变的是对规则的追求,没有一成不变的模数,也没有一成不变的比例,黄金分割也只不过是一种习惯,即使承认 1×1×1 的立方体是美的,我们也无法无端地将一个物品就设计成这个比例。
如果说最基本的一条线一个形态都由数学来决定,那么由这些线这些形态组成产品必然包含着数学。